BLUE THINK TANK

I have previously linked this article on Markov matrices as applied to baseball as a good read for the non-math geeks. Please read if you are unfamiliar with its concept.

I have discussed the value of the stolen base in 2 previous posts, on 3/30 and on 4/3. Using Dave Roberts' 04 regular season (38 out of 41) as an example, I calculated that Roberts' stolen bases were worth about 5 "expected" runs over the course of the season - not a whole lot.

In the second post, I stated that there is a difference between "winning" and "scoring runs". (The point is to win, whether by a run or 10 runs.) In a tight late inning game, the strategy is not necessarily outscoring your opponent by as many runs as possible; the team may try to eke out a single run to tie or win. So a stolen base, as with other situational plays, can make a big difference in the game's outcome.

Here is the historical "expected run matrix" for all games between 1999 and 2002, courtesy of TangoTiger. (Thanks, Tango!) It is basically the number of runs you "expect" to score given the out count and the runner situation.


Expected Runs, 99 - 02 Historical

Let's say that with no one else on, if a runner attempts to steal 2nd from 1st with 0 outs:

ExpectedRuns(0 out, runner on 1st) = 0.953
ExpectedRuns(0 out, runner on 2nd) = 1.189
Successful SB = 0.236 "expected runs" added

ExpectedRuns(0 out, runner on 1st) = 0.953
ExpectedRuns(1 out, no one one) = 0.297
Caught SB = 0.656 "expected runs" subtracted

In terms of "expected runs", a stolen base adds a mere 0.236 runs, while getting caught has a more severe penalty of minus 0.656 runs.

It's Game 4 of the ALCS, bottom of the 9th, Boston is a run down with 3 outs to go. Millar draws a walk. Runner on 1st with 0 outs. Dave Roberts enters the game as the pinch runner. A stolen base would add 0.236 "expected runs". Not a whole lot - But:

What is the probability of winning this game? How much would a stolen base help? To calculate this, I once again dug into TangoTiger's website. Here are some of the historical probabilities of scoring a certain number of runs given the out/base situation. I have it broken down another way:

Score zero runs -

Scoring 0 Runs, 99 - 02 Historical

Score a single run -

Scoring 1 Run, 99 - 02 Historical

Score 2 or more runs -

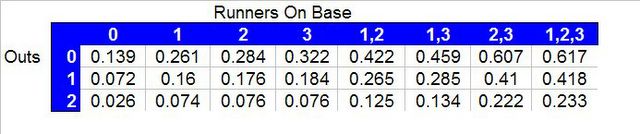
Scoring 2+ Runs, 99 - 02 Historical

(I realize that these numbers are historical "average" numbers and don't figure for the dominance of Rivera on the mound nor the strength of the batter, but they're worth looking at, nonetheless.)

In the bottom of the 9th while down by a single run with no outs and a runner at 1st, Boston can win the game if:

1) Boston scores 2 or more runs (win for sure)
2) Boston scores one run to tie (50/50 chance of winning in extra innings)

According to these charts:

WinPct(0 outs, runner on 1st) = ScoreTwoOrMoreRuns(Win) + (1/2)*ScoreOneRun(Tie)
WinPct(0 outs, runner on 1st) = 0.261 + (1/2)*0.176
WinPct(0 outs, runner on 1st) = 34.9%

Boston has a 34.9% chance of winning with no outs and a runner on 1st. Roberts attempts to steal 2nd. Had he been caught:

WinPct(1 out, no one on) = ScoreTwoOrMoreRuns(Win) + (1/2)*ScoreOneRun(Tie)
WinPct(1 out, no one on) = 0.072 + (1/2)*0.101
WinPct(1 out, no one on) = 12.2%

It's a good thing he wasn't caught. That's where Roberts' basestealing skills (92.7% success rate in 04) certainly factor in. He makes it under a close tag. Now the situation:

WinPct(0 outs, runner on 2nd) = ScoreTwoOrMoreRuns(Win) + (1/2)*ScoreOneRun(Tie)
WinPct(0 outs, runner on 2nd) = 0.284 + (1/2)*0.348
WinPct(0 outs, runner on 2nd) = 45.8%

Roberts' stolen base increased his team's chance of winning by almost 11%, which is substantial. Everyone knows what happened at this point. Dave Roberts - forever the folk hero in Beantown with a measly 0.236 "expected runs" gained.

Situational moves such as a stolen base can make a big difference in a close game, even though they may be worth little to overall run production during the course of the season.

EDIT: I finished this post in a hurry due to a dinner reservation on Saturday. As the commenters point out, there is plenty I am leaving out. Studes' article on "Win Expectancy" gives a more general (and better worded) description over at The Hardball Times.